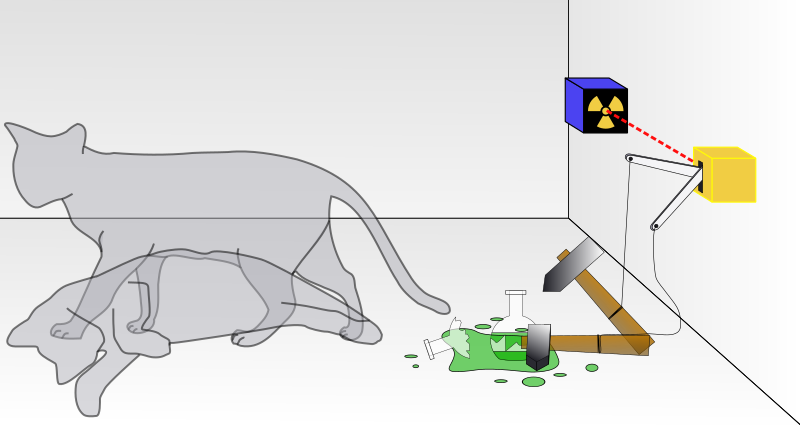
Schroedinger's cat is a normal cat

Schroedinger's Cat thought experiment is an extreme example of applying quantum mechanics to macroscopic objects, where naive quantum mechanics interpretation appears to contradict common sense.

Schrödinger's Cat: A cat, a flask of poison and a radioactive source are placed in a sealed box. If an internal monitor detects radioactivity, the flask is shattered, releasing the poison that kills the cat. The Copenhagen interpretation of quantum mechanics implies that after a while, the cat is simultaneously alive and dead. Yet, when we look in the box, we see the cat either alive or dead, not both alive and dead.

The textbook interpretation ( Copenhagen interpretation ) says, the cat+radioactive source is in an entangled state until one opens the box (measurement):
\[
\left.| \text{system} \right> = \frac{1}{\sqrt{2}} \left( \left.| : ) \right> \left.| 0 \right> + \left.| :( \right> \left.| 1 \right> \right)
\]
Entanglement implies the cat is both alive and dead before the box opened. But the application of quantum entanglement to a macro object, here cat, is controversial. In fact, the purpose of Schroedinger is to illustrate that quantum state (eps. wavefunction) may not be legitimate for describe macro system.

It's undoubted that there is something we don't know in the box, due to the quantum nature of radioactivity. But lack of information should be distinguished from quantum uncertainty.  In the sense of classical information theory, Schrodinger's cat is merely a normal cat. It's in some definite state (alive or dead). Yet different observers have different information: the experimenter said I don't know; while the flea on the back of the cat (or the cat itself) clearly knows what happened. There are many things in this world we don't know. A lot of them are associated with some quantum mechanical object (such as atoms emitting light). But we don't say, they are entangled.

It might be possible some day, the classical uncertainly and the quantum uncertainly are unified in a weird way, just like many other interpretation of quantum mechanics hoped. But in Schroedinger's Cat experiment, they are different. The main point is that the classical uncertainty is artificial. The cat is a macro object, meaning that it has huge amount of particle exchange with the environment. Outside the box, we can hear for example its scratch  sound. It's possible that the sound wave is overwhelmed by the noise, or our ears are not good enough. In either case, there exists a threshold $E_c$. Let's assume the cat-poison-radioactivity can be treated in a quantum mechanical way (See the Feynman diagram below). We can calculate the amplitudes $\mathcal{T}_{fi}$.

Notice that the cat must have interaction with the environment, we must also include such diagrams:

The sound etc. made by the cat is  characterized by $E$, $E_c$ is the threshold of the detector. 

The correction has similar structure with QED soft bremsstrahlung. In fact, we can assume the interaction of cat via environment is via QED ( for example, we can put a charge on the cat, and detect the electric field stirring outside the box). Let's simply borrow QED soft bremsstrahlung correction formula:
\[
 T'_{fi} = T^{(0)}_{fi} \cdot \exp\{ - f ( E / E_c) \}
\]
where $f(x)$ is increasing function.

The meaning of the result is, for a macro object, the correction always exist. In the case of an infinitely accurate detector, the classical cat and quantum cat cannot be distinguished by experiment. However, the amplitude is zero, i.e. still we can distinguish the classical cat and the quantum cat.