Symmetric Sparse Matrix
Sparse matrices are the matrices populated primarily with zeros. Iterative linear solvers, such as the Lanczos-Arnoldi procedure, are among the most important computational tools for solving large symmetric (Hermitian) sparse linear problems. The fundamental operation in the iterative methods is the sparse matrix vector multiplication (SpMV).
Sparse matrix can be stored in several formats. The most flexible one is the coordinate storage scheme (COO). In this scheme, one use three arrays (two integral and one scalar):
In this scheme, the $n_p$ processors are aligned as a $n_d \times n_d$ 2D grid. For symmetric matrices, only half of the grid is needed. Then, for $n_p$ processors, $ n_d (n_d + 1)/2 \le n_p \implies n_d \le \text{floor}\left( \frac{\sqrt{1+n_p}-1}{2}\right)$. It is useful to assign each processor a 2D coordinate $(I, J)$, where $I,J = 1,2,3,\cdots, n_d$. We will discuss the processor assignment later.
The vector $x$ is stored on the diagonal and the matrix $A$ is distributed across the processor grid. More specifically, vector element $x_i$ is stored in processor $(I, I)$, where $I = \mod(i, n_d) + 1$. Matrix element $A_{ij}$ is distributed to processor $(I, J)$, $I = \mod(i, n_d)+1, J = \mod(j,n_d)+1$, forming a local block matrix $A_{IJ}$.
The local blocks need not be square matrix, except the diagonal blocks. Let $n_I$ be the dimensionality of the $I$-th diagonal blocks. It is easy to see, the row and column dimensionality of the block $A_{IJ}$ is $n_I$ and $n_J$, respectively. \[ n_I = \text{floor}\left(\frac{n-1}{n_d}\right) + \vartheta\left(n-\text{floor}\left(\frac{n-1}{n_d}\right)\cdot n_d - I \ge 0\right) \]
Matrix block $A_{IJ}$ is on processor $ p = F(I-J-1)+J-1$, where $F(x) = (x+1) (2 n_d - x)/2$. In practice, one knows the local process id $p$ and wants to determine which matrix block is stored on it: \[
\begin{split}
I &= 1+p+1+G(p+1)-F(G(p+1)-1); \\
J &= p+1-F(G(p+1)-1).
\end{split}
\] where $G(x) = \text{floor}\left(n_d - \sqrt{\left(n_d+\frac{1}{2}\right)^2-2x} - \frac{1}{2}\right)$.
To store the node information, we introduce a FORTRAN module (a struct is a similar structure in C):
The problem of the DM scheme is that the number of processors in each row & column communicator is not the same. Indeed, it is not well balanced: some rows & columns have $n_d$ (ndiag) processors, some of them have only 1. This problem can be solved by using the so-called Balanced Column Major scheme.
In the BCM scheme, each row or column has $\frac{n_d+1}{2}$ blocks.
The corresponding matrix blocks distribution on processor $p$ is,
if $ p\le \text{ceiling}\left(\frac{n_d+1}{2}\right)\left[ n_d+1-\text{ceiling}\left(\frac{n_d+1}{2}\right)\right]-1$ then \[ \begin{split}
J &= \text{floor}\left(\frac{p}{\text{ceiling}\left(\frac{n_d+1}{2}\right)}\right)+1; \\ I &= \mod\left( p, \text{ceiling}\left(\frac{n_d+1}{2}\right)\right)+J;
\end{split} \]
else,
\[ \begin{split} J &= n_d+2-\text{ceiling}\left(\frac{n_d+1}{2}\right)+\text{floor}\left( \frac{q}{\text{floor}\left(\frac{n_d+1}{2}\right)}\right); \\ I &= \mod\left( \mod\left(q, \text{floor}\left(\frac{n_d+1}{2}\right)\right) +J-1, n_d\right)+1; \end{split} \] where $q = p-\text{ceiling}\left(\frac{n_d+1}{2}\right)\left[n_d+1-\text{ceiling}\left(\frac{n_d+1}{2}\right)\right]$.
The nodeinfo.mod can be modified accordingly.
\[ A x + y \to y \Rightarrow T x + (x^t L)^t + y \to y \]
Sparse matrix can be stored in several formats. The most flexible one is the coordinate storage scheme (COO). In this scheme, one use three arrays (two integral and one scalar):
row(nnz), col(nnz), mat(nnz)to store the row indices, column indices and the values of the nonzero matrix elements. It's easy to convert a coordinate storage scheme into other schemes such as the compressed column/row scheme (CCS/CRS). For SpMV, coordinate scheme is as efficient as CCS/CRS. It demands $2 n_{nz} + n_{nz}$ memory comparing with CCS/CRS $(n_{nz} + n) + n_{nz}$, where $n$ is the dimensionality of the matrix and $n_{nz}$ is the number of nonzeros, and $n^2 \gg n_{nz} \gg n$ for most useful cases. Only half of the matrix is stored, because the matrix is symmetric (Hermitian).
Serial Algorithm
subroutine SpMV(nnz, row, col, mat, n, x, y, ierr)
implicit none
! A*x + y -> y
! n is the dimension of the vector x, y
! nnz is the number of nonzeros
integer, intent(in) :: nnz, n, row(nnz), col(nnz)
double precision, intent(in) :: mat(nnz), x(n)
double precision, intent(inout) :: y(n)
integer, intent(out) :: ierr
integer :: i
do i = 1, nnz
y(row(i)) = y(row(i)) + mat(i)*x(col(i))
if(row(i) .ne. col(i)) then
y(col(i)) = y(col(i)) + x(row(i))*conjg(mat(i))
end if
end do
ierr = 0
end subroutine
Parallel Algorithm
Here we only talk about MPI parallelism. In reality, it is most efficient to use both MPI and OpenMP. The OpenMP parallelism can be used in the series part.
2D cyclic distribution
A parallel SpMV depends on the the distribution of the processors across the processors. 1D distribution has a serious load balancing problem. An simple and popular scheme is the 2D cyclic distribution. 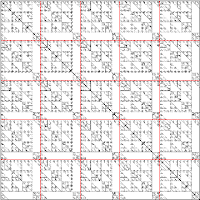  |
| Left: A naive 2D distribution. Center: A cyclic 2D distribution. Right: A cyclic 2D distribution with non-square block matrices. |
The vector $x$ is stored on the diagonal and the matrix $A$ is distributed across the processor grid. More specifically, vector element $x_i$ is stored in processor $(I, I)$, where $I = \mod(i, n_d) + 1$. Matrix element $A_{ij}$ is distributed to processor $(I, J)$, $I = \mod(i, n_d)+1, J = \mod(j,n_d)+1$, forming a local block matrix $A_{IJ}$.
The local blocks need not be square matrix, except the diagonal blocks. Let $n_I$ be the dimensionality of the $I$-th diagonal blocks. It is easy to see, the row and column dimensionality of the block $A_{IJ}$ is $n_I$ and $n_J$, respectively. \[ n_I = \text{floor}\left(\frac{n-1}{n_d}\right) + \vartheta\left(n-\text{floor}\left(\frac{n-1}{n_d}\right)\cdot n_d - I \ge 0\right) \]
Processor Assignment: Diagonal Major (DM) Scheme
In the DM scheme, the processors are assigned to the matrix blocks according to their diagonal coordinate:\begin{split}
I &= 1+p+1+G(p+1)-F(G(p+1)-1); \\
J &= p+1-F(G(p+1)-1).
\end{split}
\] where $G(x) = \text{floor}\left(n_d - \sqrt{\left(n_d+\frac{1}{2}\right)^2-2x} - \frac{1}{2}\right)$.
To store the node information, we introduce a FORTRAN module (a struct is a similar structure in C):
module nodeinfo
implicit none
integer :: nproc, myrank, myrow, mycol, ndiag, idiag;
integer :: proc_comm, row_comm, col_comm;
contains
subroutine initnodeinfo
use mpi
implicit none
integer :: ierr
! determine ndiag, nproc and rank
call mpi_comm_size(mpi_comm_world, nproc, ierr)
call mpi_comm_rank(mpi_comm_world, myrank, ierr)
ndiag = floor(0.5*sqrt(1.+8.*nproc)-0.5)
color = 0
if(ndiag*(ndiag+1)/2>rank) then
color = 1
endif
call mpi_comm_split(mpi_comm_world, color, myrank, proc_comm, ierr)
call mpi_comm_size(proc_comm, nproc, ierr)
call mpi_comm_rank(proc_comm, myrank, ierr)
! determine myrow and mycol i.e. (I,J) the block ID
mycol = 1+rank-F(G(myrank,ndiag),ndiag)
myrow = G(myrank,ndiag)+mycol+1
idiag = myrow - mycol
! create row_comm and col_comm, diag_comm
call mpi_comm_split(proc_comm, myrow, abs(idiag), row_comm, ierr)
call mpi_comm_split(proc_comm, mycol, abs(idiag), col_comm, ierr)
call mpi_comm_split(proc_comm, idiag, myrank, diag_comm, ierr)
end subroutine
integer function F(x, nd)
implicit none
integer, intent(in) :: x, nd
F = (x+1)*(2*nd-x)/2
end function
integer function G(x, nd)
implicit none
integer, intent(in) :: x, nd
G = floor(nd-0.5-sqrt((nd+0.5)**2-2*x)-0.5)
end function
integer function nloc(n, nd, i)
implicit none
integer, intent(in) :: n, nd, i
nloc = (n-1)/nd
if(n.ge.((n-1)/nd)*nd+i) then
nloc = nloc + 1
end if
end function
end module
The problem of the DM scheme is that the number of processors in each row & column communicator is not the same. Indeed, it is not well balanced: some rows & columns have $n_d$ (ndiag) processors, some of them have only 1. This problem can be solved by using the so-called Balanced Column Major scheme.
Processor Assignment: Balanced Column Major (BCM) Scheme
In the BCM scheme, each row or column has $\frac{n_d+1}{2}$ blocks.
The corresponding matrix blocks distribution on processor $p$ is,
if $ p\le \text{ceiling}\left(\frac{n_d+1}{2}\right)\left[ n_d+1-\text{ceiling}\left(\frac{n_d+1}{2}\right)\right]-1$ then \[ \begin{split}
J &= \text{floor}\left(\frac{p}{\text{ceiling}\left(\frac{n_d+1}{2}\right)}\right)+1; \\ I &= \mod\left( p, \text{ceiling}\left(\frac{n_d+1}{2}\right)\right)+J;
\end{split} \]
else,
\[ \begin{split} J &= n_d+2-\text{ceiling}\left(\frac{n_d+1}{2}\right)+\text{floor}\left( \frac{q}{\text{floor}\left(\frac{n_d+1}{2}\right)}\right); \\ I &= \mod\left( \mod\left(q, \text{floor}\left(\frac{n_d+1}{2}\right)\right) +J-1, n_d\right)+1; \end{split} \] where $q = p-\text{ceiling}\left(\frac{n_d+1}{2}\right)\left[n_d+1-\text{ceiling}\left(\frac{n_d+1}{2}\right)\right]$.
The nodeinfo.mod can be modified accordingly.
The Parallel SpMV Algorithm Based on the 2D cyclic Distribution
$A = L + D + L^t$, where $L$ is a strict lower triangular matrix and $D$ is a diagonal matrix. $T = L+D$.\[ A x + y \to y \Rightarrow T x + (x^t L)^t + y \to y \]
subroutine SpMV(nnz, row, col, mat, ncol, x, yt, nrow, y, xt, ierr)
use nodeinfo
use mpi
implicit none
! A*x + y -> y
! A = L + D + L^t, where L is a strict lower triangular matrix,
! D is a diagonal matrix, L^t is the transpose of L.
! Let T = L+D; A = T + L^t.
! A*x = T*x + L^t*x = T*x + (x^t*L)^t
!
! x/y is the local vector. Only x/y on the diagonal are initialized/output
! xt/yt is the local vector of the transpose vector of x/y
! note their local dimensionalities nrow, ncol are not the same as the original vector.
integer :: nnz, ncol, nrow, ierr, row(nnz), col(nnz);
double precision :: x(ncol), yt(ncol), y(nrow), xt(nrow), mat(nnz);
intent(in) :: nnz, ncol, nrow, row, col, mat;
! (L+D)*x + y -> y
call mpi_bcast(x, ncol, mpi_real8, 0, col_comm, ierr)
! local SpMV
if(idiag.eq.0) then
xt = y
end if
do i = 1, nnz
xt( 1+(row(i)-1)/ndiag ) = xt( 1+(row(i)-1)/ndiag ) + mat(i)*x( 1+(col(i)-1)/ndiag )
end do
call mpi_reduce(xt, y, nrow, mpi_real8, mpi_sum, 0, row_comm, ierr)
! x^t * L -> y^t
if(idiag.eq.0) then
xt = x
x = y
end if
call mpi_bcast(xt, nrow, mpi_real8, 0, row_comm, ierr)
! local SpMV
do i = 1, nnz
if( row(i) .eq. col(i) ) then
x( 1+(col(i)-1)/ndiag ) = x( 1+(col(i)-1)/ndiag ) + xt( 1+(row(i)-1)/ndiag )*conjg(mat(i))
end if
end do
call mpi_reduce(x, yt, ncol, mpi_real8, mpi_sum, 0, col_comm, ierr)
if(idiag.eq.0) then
y = y + yt
x = xt
endif
end subroutine


No comments:
Post a Comment