Schwinger Effect
According to quantum field theory, vacuum, the state of no nothingness, is actually filled with virtual particles. In particular, virtual electron and positron pairs are created and annihilated in short time and distance: \[\Delta t \sim \frac{h}{2m_ec^2} \simeq 10^{-21} \,\mathrm{s}, \quad \Delta x \sim \frac{h}{2m_ec} \simeq 10^{-12} \,\mathrm{m}. \]
 |
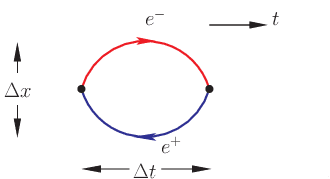| Fig. 1: Vacuum fluctuation into electron-positron pair. |
Then, it is no surprise that if we exert a strong electric field $\vec E$ on the vacuum, the virtual electron and positron would be pulled in the opposite direction. As a net result, real electron and positron pairs can be created out of vacuum. Of course, the electric field has to be strong, to provide enough energy ($\gtrsim 2m_e c^2$) for the pair production. We can do an estimation as following. In order to create real particles, the electron and positron have to be pulled apart by at least one Compton length $\lambda_e = \frac{\hbar}{m_e c}$ (so that their wave packets do not overlap much). Over such a distance, the energy provided by the electric field is, $e E \lambda_e \ge 2 m_e c^2$. Therefore the threshold electric field is \[
E_\mathrm{th} \triangleq \frac{2 m_e c^3}{e\hbar} \simeq 10^{18} \, \mathrm{V/m}.
\]
 |
| Fig. 2: The Schwinger effect. |
 |
| Fig. 3: The mass gap. The $x$-axis is the separation between the electron and its hole. Due to zitterbewegung, this distance can not be smaller than the Compton length. |
Therefore, the creation of an electron (and the positron - the hole in the Dirac sea) can be viewed as a quantum tunneling process (Fig. 3). Then the external electric field turns the well to a barrier. The width of the barrier is proportional to $w \sim 2 m_e c^2/E$. According to WKB, the tunneling probability is \[
P \sim \exp\Big( - w \sqrt{2 m_e \times e (2m_e c^2) } \Big) \simeq \exp\Big( - E_\mathrm{th}/E \Big)
\]
 |
| Fig. 4: The electric field term the mass well to a barrier. |
Super Critical Charge
We have seen in the last section that strong electric field can create electron-positron pairs out of vacuum. The Coulomb potential have a field strength proportional to $1/r^2$: $eE(r) = \frac{Z\alpha}{\hbar c r^2}$. Very close to the charge, the electric field would be extremely intense. So, it is natural to ask, if/why not such a phenomenon can be seen around a point charge. To achieve the threshold strength, the distance $r_\mathrm{th} = \sqrt{\frac{1}{2}Z\alpha} \lambda_e \simeq \sqrt{Z/2} \times 10^{-13}\,\mathrm{m}$ has to be large than the smallest distance between two particles.
For poin-like charged particles, such as electron, muons, the smallest distance is determined by 1). their Compton wavelength (zitterbewegung) $\lambda_\ell = \frac{m_e}{m_\ell}\lambda_e$; 2). the size of the bound state $\frac{m_\ell}{m\ell+m_e}\lambda_e/(Z\alpha)$. For electron/positron, this distance $r_\mathrm{th} = \sqrt{\alpha/2} \lambda_e$ is much smaller than their Compton wavelength. Therefore, even if such a phenomenon exists, it is included in the quantum fluctuation of the particle itself. Muon is about 207 times heavier than the electron. So its Compton wavelength is 207 times smaller than electron's. Then it is possible to produce a pair of real electron-positron. But as the pair were produced, the positron would be bound with the muon, forming a $\mu^-e^+$ atom. However, the ground state radius of this atom $r \simeq a_0 = \lambda_e / \alpha \gg r_\mathrm{th}$. In other words, there is no enough energy to produce the electron-positron pair. Similar cases happen for other leptons.
For composite systems, the charge factor $Z$ can be rather large. As a result, the possible bound state radius would decrease and the threshold radius increase (while the Compton wavelength remains the same). At some critical charge factor $Z_c \simeq 2/\alpha = 274$, the system would have enough energy to produce the electron-positron pair.
E_{n,j} = mc^2 \left[ 1 + \frac{Z^2\alpha^2}{\left[n-j-\frac{1}{2} + \sqrt{(j+\frac{1}{2})^2-Z^2\alpha^2}\right]^2} \right]^{-1/2}
\] where $n = 1, 2, 3, \cdots$ is called the principal quantum number and $j=1/2, 3/2, 5/2, \cdots n-1/2$ is the total angular momentum. As we can see, for the S-state ($j=1/2$), the energy becomes imaginary if $Z > 1/\alpha \simeq 137$. This is half of the critical charge we found above using a crude estimate.
The existence of imaginary energy eigenvalues implies the Dirac Hamiltonian is no longer Hermitian as Dirac promised. Something is wrong. The solution of the Dirac equation does not represent the motion of an electron. Instead, given the time-dependent part $\exp\big(- |E|t \big)$, it represents the amplitude of some tunneling process.
Even though Dirac's theory is broken at $Z>137$, we can still mill some plausible physics out of it, invoking the Dirac sea -- as one may have noted, the creation of particles in the Dirac theory always involves the Dirac sea. It turns out, at the presence of the super critical charge, the Coulomb level dives into the Dirac sea. Therefore, the electrons at the Dirac sea jump down to Coulomb levels below and leave holes in the Dirac sea, manifested as the positron (see Fig. 6). This interpretation can be elaborated (including using other methods) to give the semi-quantitative dynamics of the process.
In QED, the vacuum is the ground state of the charge-zero sector:\[
H_\mathrm{QED} |\Omega\rangle = E_\Omega |\Omega\rangle
\] Here $H_\mathrm{QED}$ is the QED Hamiltonian. $E_\Omega$ is the vacuum energy. It can be renormalized to 0.
In our problem, there exists a charged heavy ion $Z^+$, which generates an strong electromagnetic field $\mathcal A$. With the presence of this field, the ground state may be different: \[
\big( H_\mathrm{QED} + J_\mu \mathcal A^\mu \big) |\Omega_{\mathcal A}\rangle = E_\mathcal{A} |\Omega_{\mathcal A}\rangle
\] Where $|\Omega_{\mathcal A}\rangle$ represents the polarized QED vacuum within field $\mathcal A^\mu$, $J^\mu = e\bar\psi \gamma^\mu \psi$ is the fermion charge current.
If the charge of the heavy ion is subcritical, the polarized vacuum only involves the photon loop-correction and electron loop-corrections (see Fig. 7), which can be taken into account by renormalization (UV renormalization and the bremsstrahlung) of the heavy ion. When the mass of the heavy ion is sufficiently large, the renormalization effects can be neglected. When the charge of the heavy ion $Z^+$ exceeds some critical value $Z_c$, a new vacuum state emerges. It consists a free positron and a $Z^+e^-$ bound-state. Such a vacuum state is called a charged vacuum. Dynamically, we see the spontaneous production of an electron-positron pair.
In practice, the matrix can be truncated to the first few sector to retain the minimal physical of the charged vacuum (See Fig. 9). The minimal sector should include at least one photon and one pair of electron and positron.
We can further suppress the heavy ion sector and treat the field it generates simply as a classical external field. In this way the charged vacuum is more qualified for its name. (Otherwise it is just the ground state of the supercritical charge sector.)
The charged vacuum can also be studied within the path integral formalism. According to this formalism, the vacuum expectation value of an operator within the external field is, simply, \[
\langle \mathrm T\mathcal O_\psi \rangle_{\mathcal A} = \int \mathcal D_{\psi,\bar\psi, \mathcal A} \, \mathcal O_\psi \, \exp\Big[ i\int d^4x \, \bar \psi(x) \big( i\gamma^\mu D_\mu - m\big) \psi(x)\Big]
\] where $D_\mu = \partial_\mu - ie\mathcal A_\mu$.
Both the matrix diagonalization and the path integral methods are non-perturbative. But different approximation may arise for each formalism. We shall not delve into those lengthy technologies but only mention one famous result due to Schwinger. Let's consider the production rate, which is related to the vacuum decay probability: $P = 1 - |\langle\Omega_{\mathcal A}|\Omega_{\mathcal A}\rangle|^2 \approx 1 - \exp( -2 \mathrm{Im} S_\mathrm{eff})$. Here Schwinger applied an approximation: $\langle\Omega_{\mathcal A}|\Omega_{\mathcal A}\rangle = \det^{-1} \bar\psi \big( i\gamma^\mu D_\mu - m\big) \psi \approx \exp(i S_\mathrm{eff})$. $S_\mathrm{eff}=\int d^4x\,\mathcal L_\mathrm{eff}$ is called the effective action. The one-loop effective action was calculated obtained Heisenberg and Bonn. Plug into this effective action, and assuming a uniform electric field $E$, Schwinger's conclusion for the vacuum pair production rate is, \[
R \triangleq \frac{dN}{dVdt} = \frac{(eE)^2}{4\pi^3}\sum_{n=1}^\infty \frac{1}{n^2} \exp\big( -n\pi E_c/E\big)
\] where $E_c \triangleq m_e^2 c^3/(e\hbar) \sim 10^{18} \,\mathrm{V/m}$ is the critical electric field. This formulation is the famous Schwinger mechanism of vacuum pair production.
One can also solve the Schroedinger's equation directly, starting for example, from the normal QED vacuum state: \[
i \frac{\partial}{\partial t} |\psi(t)\rangle = \big( H_\mathrm{QED} + J^\mu \mathcal A_\mu\big) | \psi(t)\rangle, \quad
|\psi(0)\rangle = |\Omega\rangle.
\] In this way, the time evolution of the QED vacuum can be studied. This approach is also non-perturbative.
In the above description, we deliberately avoid the photon mediated electron-positron interaction. This can be included by the quantized electromagnetic field $A^\mu$. So the full covariant derivative can be written as $D_\mu = \partial_\mu - i e\mathcal A_\mu - ie A_\mu$. Note that this field is small comparing with the external field $\mathcal A$ generated by the supercritical heavy ion, $|\mathcal A| \sim Z |A|$. In practice, the correction due to quantized photon can be included through the usual perturbation theory.
For poin-like charged particles, such as electron, muons, the smallest distance is determined by 1). their Compton wavelength (zitterbewegung) $\lambda_\ell = \frac{m_e}{m_\ell}\lambda_e$; 2). the size of the bound state $\frac{m_\ell}{m\ell+m_e}\lambda_e/(Z\alpha)$. For electron/positron, this distance $r_\mathrm{th} = \sqrt{\alpha/2} \lambda_e$ is much smaller than their Compton wavelength. Therefore, even if such a phenomenon exists, it is included in the quantum fluctuation of the particle itself. Muon is about 207 times heavier than the electron. So its Compton wavelength is 207 times smaller than electron's. Then it is possible to produce a pair of real electron-positron. But as the pair were produced, the positron would be bound with the muon, forming a $\mu^-e^+$ atom. However, the ground state radius of this atom $r \simeq a_0 = \lambda_e / \alpha \gg r_\mathrm{th}$. In other words, there is no enough energy to produce the electron-positron pair. Similar cases happen for other leptons.
 |
| Fig. 5: The electron-positron pair production by a muon. This process is kinematically forbidden. |
For composite systems, the charge factor $Z$ can be rather large. As a result, the possible bound state radius would decrease and the threshold radius increase (while the Compton wavelength remains the same). At some critical charge factor $Z_c \simeq 2/\alpha = 274$, the system would have enough energy to produce the electron-positron pair.
Again, Dirac Sea
To give a little bit quantitative touch, let's turn to the Dirac theory again (We don't turn to Schroedinger's theory because at the super critical charge, the system is relativistic.). The Dirac equation with a Coulomb potential produces the energy spectrum (Sommerfeld fine-structure formula): \[E_{n,j} = mc^2 \left[ 1 + \frac{Z^2\alpha^2}{\left[n-j-\frac{1}{2} + \sqrt{(j+\frac{1}{2})^2-Z^2\alpha^2}\right]^2} \right]^{-1/2}
\] where $n = 1, 2, 3, \cdots$ is called the principal quantum number and $j=1/2, 3/2, 5/2, \cdots n-1/2$ is the total angular momentum. As we can see, for the S-state ($j=1/2$), the energy becomes imaginary if $Z > 1/\alpha \simeq 137$. This is half of the critical charge we found above using a crude estimate.
The existence of imaginary energy eigenvalues implies the Dirac Hamiltonian is no longer Hermitian as Dirac promised. Something is wrong. The solution of the Dirac equation does not represent the motion of an electron. Instead, given the time-dependent part $\exp\big(- |E|t \big)$, it represents the amplitude of some tunneling process.
Even though Dirac's theory is broken at $Z>137$, we can still mill some plausible physics out of it, invoking the Dirac sea -- as one may have noted, the creation of particles in the Dirac theory always involves the Dirac sea. It turns out, at the presence of the super critical charge, the Coulomb level dives into the Dirac sea. Therefore, the electrons at the Dirac sea jump down to Coulomb levels below and leave holes in the Dirac sea, manifested as the positron (see Fig. 6). This interpretation can be elaborated (including using other methods) to give the semi-quantitative dynamics of the process.
 | |
|
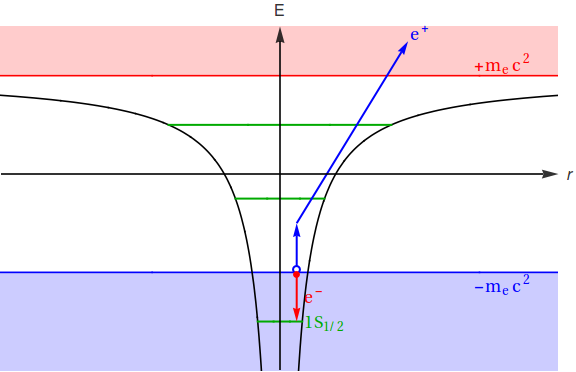QED with Strong External Fields
This problem can also be described by QED. Unlike the Dirac theory, the QED Hamiltonian is always Hermitian. Hence a self-consistent quantitative description of the problem has come from QED.In QED, the vacuum is the ground state of the charge-zero sector:\[
H_\mathrm{QED} |\Omega\rangle = E_\Omega |\Omega\rangle
\] Here $H_\mathrm{QED}$ is the QED Hamiltonian. $E_\Omega$ is the vacuum energy. It can be renormalized to 0.
In our problem, there exists a charged heavy ion $Z^+$, which generates an strong electromagnetic field $\mathcal A$. With the presence of this field, the ground state may be different: \[
\big( H_\mathrm{QED} + J_\mu \mathcal A^\mu \big) |\Omega_{\mathcal A}\rangle = E_\mathcal{A} |\Omega_{\mathcal A}\rangle
\] Where $|\Omega_{\mathcal A}\rangle$ represents the polarized QED vacuum within field $\mathcal A^\mu$, $J^\mu = e\bar\psi \gamma^\mu \psi$ is the fermion charge current.
If the charge of the heavy ion is subcritical, the polarized vacuum only involves the photon loop-correction and electron loop-corrections (see Fig. 7), which can be taken into account by renormalization (UV renormalization and the bremsstrahlung) of the heavy ion. When the mass of the heavy ion is sufficiently large, the renormalization effects can be neglected. When the charge of the heavy ion $Z^+$ exceeds some critical value $Z_c$, a new vacuum state emerges. It consists a free positron and a $Z^+e^-$ bound-state. Such a vacuum state is called a charged vacuum. Dynamically, we see the spontaneous production of an electron-positron pair.
  |
| Fig. 7: The QED vacuum within the subcritical (top) and supercritical (bottom) external field. The double line represent the heavy ion with a positive subcritical charge. The single line loop represents the electron/positron loop correction. The wavy lines represents the photons. The dot represents the coupling between the photon and the super critical charge. The blue single line represents the emitted positron. The red single line represents the bound electron. |
In practice, the matrix can be truncated to the first few sector to retain the minimal physical of the charged vacuum (See Fig. 9). The minimal sector should include at least one photon and one pair of electron and positron.
 |
| Fig. 9: The QED matrix within the first few Fock sectors. The vertex with a dot represents the super critical charge coupling $Ze$. |
 | |
|
\langle \mathrm T\mathcal O_\psi \rangle_{\mathcal A} = \int \mathcal D_{\psi,\bar\psi, \mathcal A} \, \mathcal O_\psi \, \exp\Big[ i\int d^4x \, \bar \psi(x) \big( i\gamma^\mu D_\mu - m\big) \psi(x)\Big]
\] where $D_\mu = \partial_\mu - ie\mathcal A_\mu$.
Both the matrix diagonalization and the path integral methods are non-perturbative. But different approximation may arise for each formalism. We shall not delve into those lengthy technologies but only mention one famous result due to Schwinger. Let's consider the production rate, which is related to the vacuum decay probability: $P = 1 - |\langle\Omega_{\mathcal A}|\Omega_{\mathcal A}\rangle|^2 \approx 1 - \exp( -2 \mathrm{Im} S_\mathrm{eff})$. Here Schwinger applied an approximation: $\langle\Omega_{\mathcal A}|\Omega_{\mathcal A}\rangle = \det^{-1} \bar\psi \big( i\gamma^\mu D_\mu - m\big) \psi \approx \exp(i S_\mathrm{eff})$. $S_\mathrm{eff}=\int d^4x\,\mathcal L_\mathrm{eff}$ is called the effective action. The one-loop effective action was calculated obtained Heisenberg and Bonn. Plug into this effective action, and assuming a uniform electric field $E$, Schwinger's conclusion for the vacuum pair production rate is, \[
R \triangleq \frac{dN}{dVdt} = \frac{(eE)^2}{4\pi^3}\sum_{n=1}^\infty \frac{1}{n^2} \exp\big( -n\pi E_c/E\big)
\] where $E_c \triangleq m_e^2 c^3/(e\hbar) \sim 10^{18} \,\mathrm{V/m}$ is the critical electric field. This formulation is the famous Schwinger mechanism of vacuum pair production.
One can also solve the Schroedinger's equation directly, starting for example, from the normal QED vacuum state: \[
i \frac{\partial}{\partial t} |\psi(t)\rangle = \big( H_\mathrm{QED} + J^\mu \mathcal A_\mu\big) | \psi(t)\rangle, \quad
|\psi(0)\rangle = |\Omega\rangle.
\] In this way, the time evolution of the QED vacuum can be studied. This approach is also non-perturbative.
 |
| Fig. 11: the same diagrams as Fig. 10, but taking into account the quantized photons. The external fields are represented as double wavy lines. The real photon lines are the single wavy lines. |
Pair Production in the Relativistic Heavy Ion Collisions
Experiments
[ To Be Continued ... ]
References:
[1]: W. Greiner, B. Muller and J. Rafelski, Quantum electrodynamics of strong fields, (1985) Springer-Verlag, Berlin Heidelberg.
No comments:
Post a Comment